VM2: Rigorous Inclusion of Entropy
The Importance of Entropy
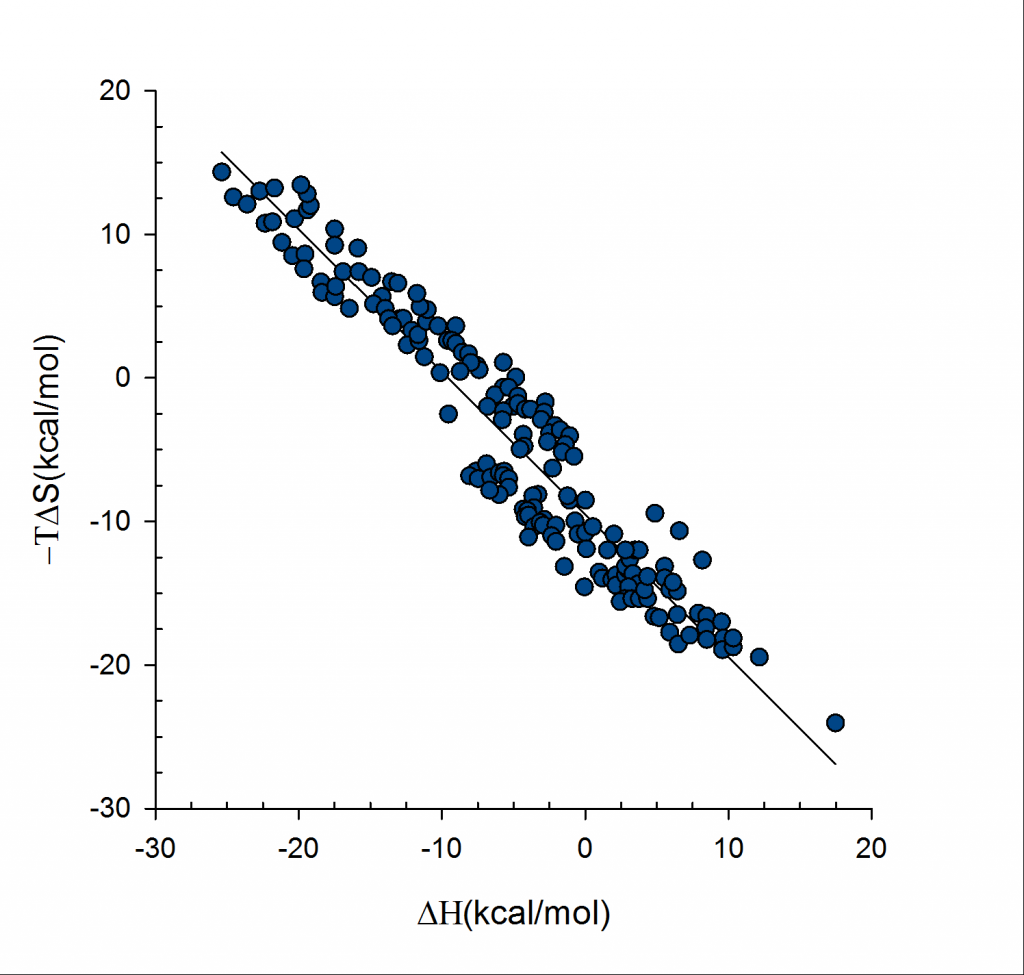
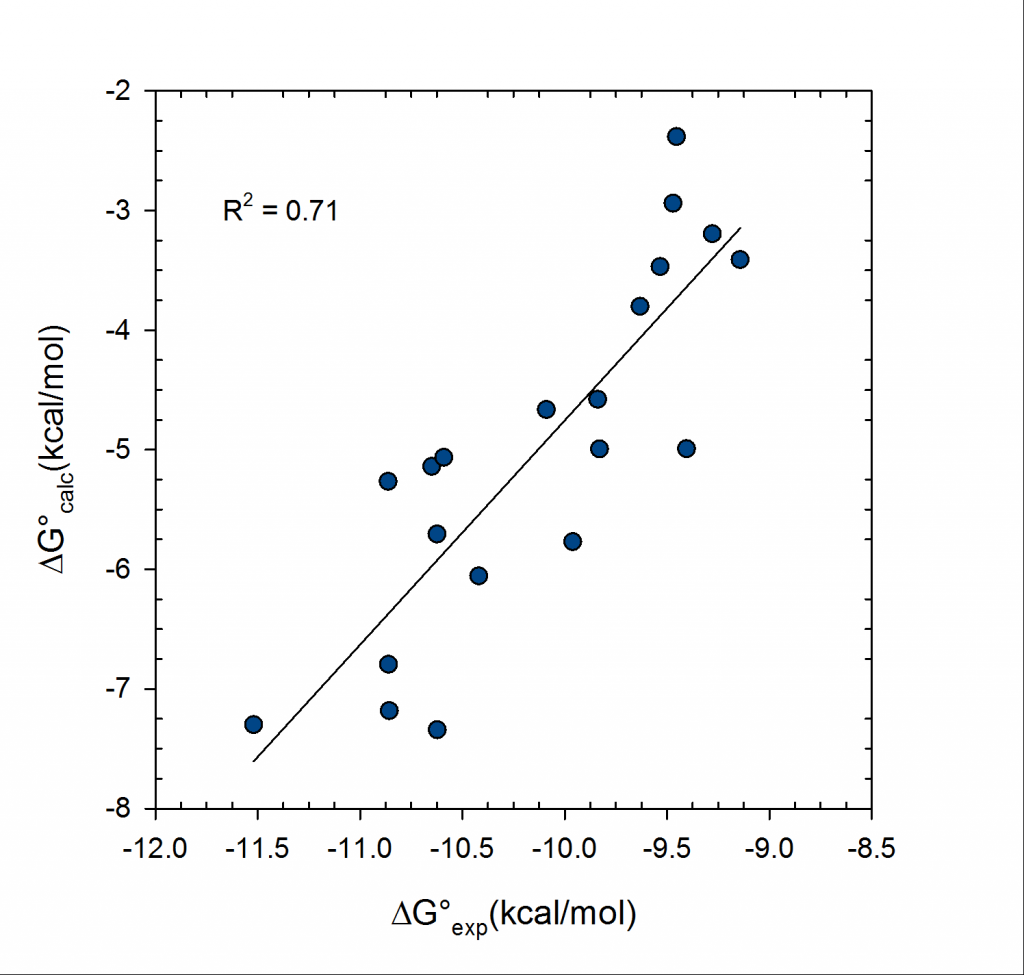
This plot demonstrates entropy-enthalpy compensation found in experimental binding data – source BindingDB. That is, the stronger the enthalpy of binding the larger the entropy penalty paid. This is physically reasonable as a more strongly interacting ligand will be more immobilized as will the protein active site, resulting in a loss of entropy. However, the graph is not perfectly linear i.e. there is a width to the slope, and so enthalpy changes cannot be relied on exclusively to provide accurate ordering of binding affinities and entropy terms should also be included.
These two plots further demonstrate the need for entropy inclusion for accurate binding affinity prediction. On the left is the potential energy of binding from VM2 calculations is plotted against experimental binding
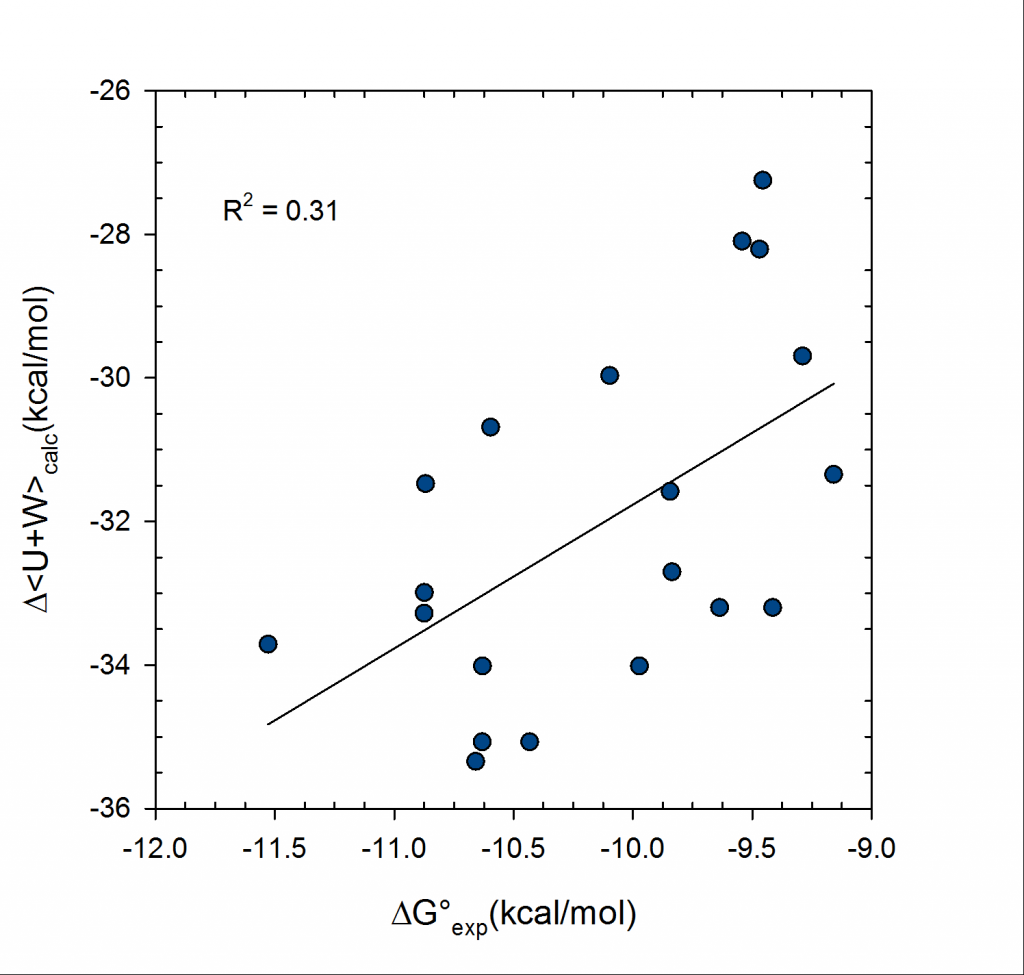
affinities i.e. entropy terms are excluded. On the right the entropy terms are included. System is PDE10a and 20 inhibitors. VM2 calculations used united atom CHARMM force field.
Theoretical Basis of VM2
Statistical thermodynamics of binding
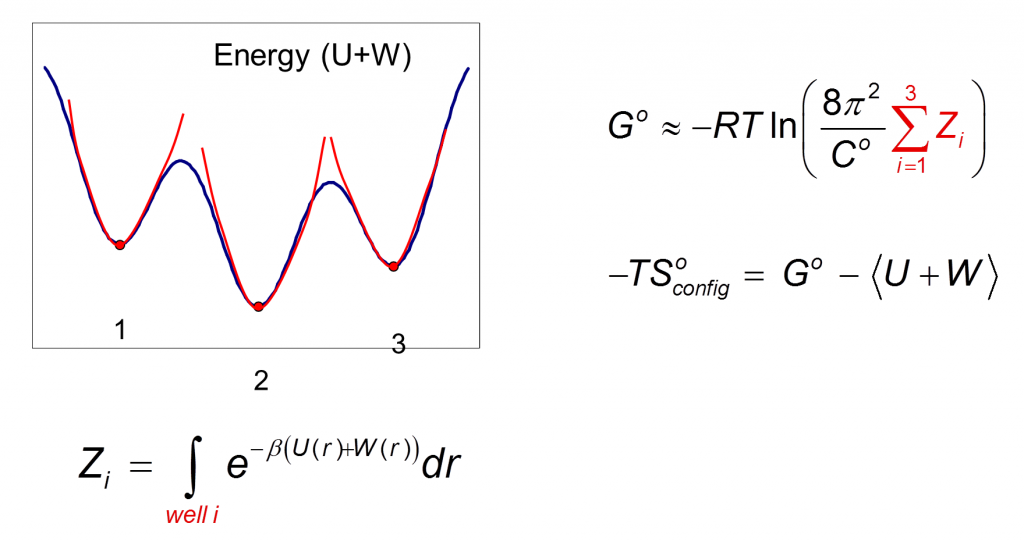
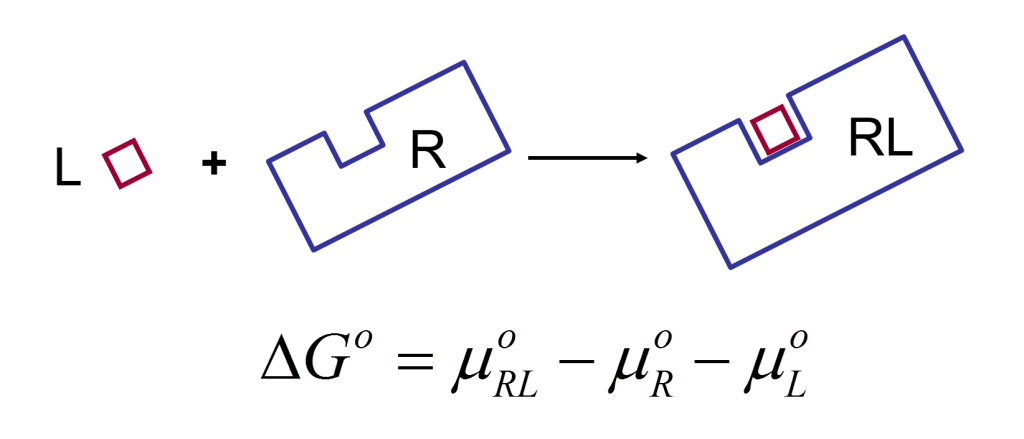
VM2 is solidly grounded in a statistical thermodynamics approach to the prediction of binding affinities. VM2 aims to predict standard free energies of binding. Experiments can determine standard binding free energies through the equilibrium constant Kbind (see below), where the equilibrium constant itself is determined via the receptor, ligand, receptor-ligand concentrations along with the standard concentration.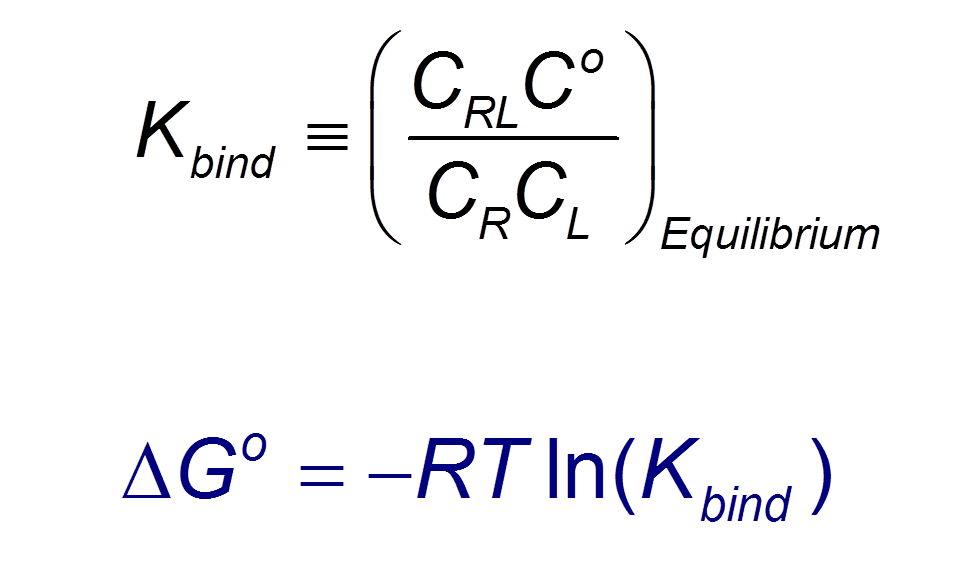
VM2 calculates the standard free energy of binding via the standard chemical potentials of the receptor, ligand, and receptor-ligand complex.
VM2 uses the classical formulation of the partition function for calculation of each chemical potential.
Here the external degrees of freedom have been integrated out and C0 provides a correction to the standard state. Formally, the configuration integral must be determined over all space along the remaining internal degrees of freedom, the VM2 method approximates this using the concept of mining minima.
Mining minima
The mining minima approach replaces the configurational integral over all space with a sum over separate local configuration integrals associated with low energy minima of the system. For example, the figure below depicts a system where three low-lying energy minima have been found.
Determination of the local configurational integrals Zi allows a probability to be associated with each energy well, and this, in turn, allows a Boltzmann averaged energy
<U+W> to be determined and subtracted from the total free energy to give the system’s configurational entropy, useful when analyzing and interpreting predicted binding affinites.
Local configuration integrals
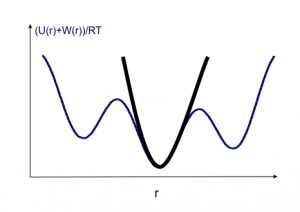
A Harmonic approximation together with a numeric correction for anharmonic low-energy modes, the Harmonic Approximation with Mode Scanning (HAMS) method, is used to calculate the local configuration integral
for each minimum produced. The harmonic approximation is applied via square roots of the Hessian matrix eigenvalues.
The Mode Scanning anharmonic corrections are calculated by numerical integration of the energy surfaces produced by distortion along low-energy internal-coordinate modes.
