About Us
VeraChem’s state of the art computational chemistry software is capable of protein-ligand and host-guest binding affinity prediction, fast calculation of accurate partial atomic charges for drug-like compounds, computation of energies and forces with empirical force fields, automatic generation of alternate resonance forms of drug-like compounds, conformational search with the powerful Tork distort-minimize algorithm, and automatic detection of topological and 3D molecular symmetries.
Recent Posts
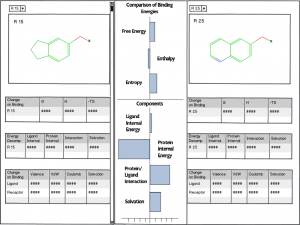
- VM2 receptor-ligand binding free energy results analysis using Chemical Computing Group’s MOE graphical user interface now available through the CCG SVL Exchange
- VeraChem is pleased to announce the release of VM2 3.0, the latest version of its software for the calculation of protein-ligand and host-guest binding free energies.
- Prof. Mike Gilson talks about VM2 for fast accurate protein-ligand binding free energies.
- A joint VeraChem, Iowa State University, and University of Colorado Denver study applying QM-VM2 to the calculation of host-guest binding free energies published in the Journal of Chemical Physics.
Contact Info
VeraChem LLC
12850 Middlebrook Rd Ste 205
Germantown
MD 20874-5244
Voice: 240-686-0565
Fax: 240-686-0564
General e-mail:
vc@verachem.com
Commercial licensing:
sales@verachem.com
Customer support:
support@verachem.com